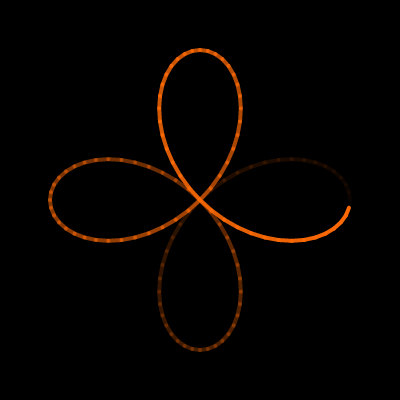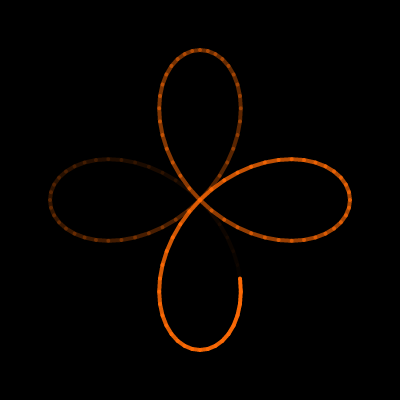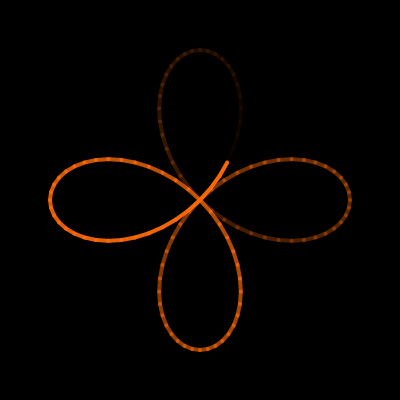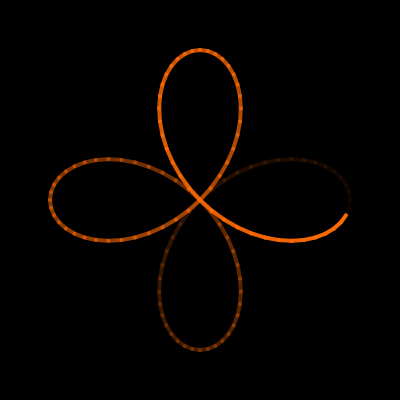I dette eksempelet skal vi forklare hvordan vi har gått frem for å lage animasjonen du ser under. Figuren som genereres er inspirert av en hypersykloide hvor den innerste sirkelen ikke nødvendigvis «ruller» på den ytterste sirkelen. Ved å trykke på animasjonene i de fire stegene blir du sendt til en ekstern side (P5JS) hvor koden er laget, slik at du kan se og eventuelt endre på koden.

Bak animasjonen ligger det skjult en veldig enkel idé. Animasjonen får vi ved å følge et punkt på en liten sirkel som ruller rundt i en større sirkel:

Steg 1:

Vi begynner med å animere et punkt som bever seg rundt sirkelperiferien.

Denne koden er skrevet i JavaScript. Se kode: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

let tid = 0; // Setter tid til en variabel
let l = 400; // Lengde på lerret
let b = 400; // bredde på lerret
let radius = (l / 2) * 0.8; // radius til sirkelen

function setup() { // Denne koden kjøres en gang for å lage lerretet vår
  createCanvas(l, b);
}

function draw() {
  background(0); // setter bakgrunnen sort
  noFill(); // nofill 
  strokeWeight(4); // setter tykkelse på linjer
  stroke("blue"); // setter farge på linjene
  circle(l / 2, b / 2, radius * 2); // lager en sirkel
  noStroke(); // fjerner linje langs kanter av figurer
  fill(255); // fyller figurer helt hvite
  circle(l / 2 + radius * cos(tid), b / 2 + radius * sin(tid), 10); // lager sirkel
  tid += 0.01 // økter tiden med 0.01. Dette gjør at punktet vårt vil rotere.
}

Steg 2:

Vi ønsker nå å ta idéen fra steg 1 til å animere en sirkel som ruller rundt i sirkelen, med ett punkt som er markert.

Denne koden er skrevet i JavaScript. Se kode: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

let tid = 0;
let l = 400;
let b = 400;
let radius = 150; // radius til store sirkel
let r2 = 75; // radius til lille sirkel
let forhold = radius / r2; // Hvor mange runder tar lille sirkelen hvis den ruller rundt 

function setup() {
  createCanvas(l, b);
  
}


function draw() {
  background(0);
  noFill(255);
  strokeWeight(4);
  stroke("blue");
  circle(l / 2, b / 2, radius * 2);
  stroke(100, 160, 60)
  strokeWeight(3);
  circle(l / 2 + (radius - r2) * cos(tid), b / 2 + (radius - r2) * sin(tid), r2 * 2);
  strokeWeight(3);

  stroke("red")
  circle(l / 2 + (radius - r2) * cos(tid) + r2 * cos(-(forhold +1) * tid), b / 2 + (radius - r2) * sin(tid) + r2 * sin(-(forhold +1) * tid),5)

  tid += 0.01
}

Steg 3:

For å lage animasjonen trenger vi å spore stien som punktet lager. Det er dette vi har gjort under.

Denne koden er skrevet i JavaScript. Se kode: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

let tid = 0;
let l = 400;
let b = 400;
let radius = 150; // radius til store sirkel
let r2 = 75; // radius til lille sirkel
let forhold = radius / r2; // Hvor mange runder tar lille sirkelen hvis den ruller rundt 
let trace = [];

function setup() {
  createCanvas(l, b);
  
}


function draw() {
  background(0);
  noFill(255);
  strokeWeight(4);
  stroke("blue");
  circle(l / 2, b / 2, radius * 2);
  stroke(100, 160, 60)
  strokeWeight(3);
  circle(l / 2 + (radius - r2) * cos(tid), b / 2 + (radius - r2) * sin(tid), r2 * 2);
  strokeWeight(3);
  for (i of trace) {
    stroke(255,107,6,255-(tid-i)*100*255/500);
    color(255,107,6,255-(tid-i)*100*255/500);
    circle(l / 2 + (radius - r2) * cos(i) + r2 * cos(-(forhold +1) * i), b / 2 + (radius - r2) * sin(i) + r2 * sin(-(forhold +1) * i), 1);
    
  }
  stroke("red")
  circle(l / 2 + (radius - r2) * cos(tid) + r2 * cos(-(forhold +1) * tid), b / 2 + (radius - r2) * sin(tid) + r2 * sin(-(forhold +1) * tid),5)
  trace.unshift(tid);
  if (trace.length>500) {
    trace.pop()
  }
  tid += 0.01
}

Steg 4:

Til slutt vil vi fjerne alt unøvendig støy, og kun la sporet være igjen. Det gir følgende animasjon.

Denne koden er skrevet i JavaScript. Se kode: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

let tid = 0;
let l = 400;
let b = 400;
let radius = 150; // radius til store sirkel
let r2 = 75; // radius til lille sirkel
let forhold = radius / r2; // Hvor mange runder tar lille sirkelen hvis den ruller rundt 
let trace = [];

function setup() {
  createCanvas(l, b);
}

function draw() {
  background(0);
  noFill(255);
  strokeWeight(4); 
  strokeJoin(ROUND);
  for (let i = 1; i < trace.length; i++) {
    stroke(255,107,6,255-(tid-trace[i])*100*255/650);
    line(l / 2 + (radius - r2) * cos(trace[i-1]) + r2 * cos(-(forhold +1) * trace[i-1]), b / 2 + (radius - r2) * sin(trace[i-1]) + r2 * sin(-(forhold +1) * trace[i-1]), l / 2 + (radius - r2) * cos(trace[i]) + r2 * cos(-(forhold +1) * trace[i]), b / 2 + (radius - r2) * sin(trace[i]) + r2 * sin(-(forhold +1) * trace[i]));  
  }
  trace.unshift(tid);
  if (trace.length>400) {
    trace.pop()
  }
  tid += 0.04*2*PI/6
}


Ekstra: Her har vi plottet høyden til punktet som grafen til en funksjon \( f(t) \).

Dette kan for eksempel være en måte å illustrere hvordan resultatet blir hvis vi kombinerer trigonometriske funksjoner.

Ekstra: Her har vi fortsatt med flere rullende sirkler inne i hverandre.